miércoles, 16 de marzo de 2016


DINÁMICA


Resultado de imagen para imagenes de dinamica en fisica

CONCEPTO


La dinámica es la parte de la física que describe la evolución en el tiempo de un sistema físico en relación con las causas que provocan los cambios de estado físico y/o estado de movimiento. El objetivo de la dinámica es describir los factores capaces de producir alteraciones de un sistema físico ed decir, la FUERZA, cuantificarlos y plantear ecuaciones de movimiento o ecuaciones de evolución para dicho sistema de operación.

 DESARROLLO HISTÓRICO 

El estudio de la dinámica fue iniciada por Aristóteles en torno a 384 aC. Aristóteles desarrolló una teoría en un intento de explicar los movimientos de los cuerpos. Esta teoría sigue siendo válida hasta la Edad Media, más precisamente en la época del Renacimiento. Aristóteles es considerado hoy, el precursor de Galileo Galilei, teniendo sus ideas Una de las máximas descubiertas por el antiguo pensador fue la siguiente: el movimiento puede existir sin la existencia de las fuerzas externas que actúan sobre el cuerpo. Por ejemplo, un disco de hockey cae sobre una superficie completamente lisa y en la ausencia de resistencia del aire, puede mantener su estado de movimiento de forma indefinida.
Isaac Newton y las leyes del movimiento
Newton, el científico Inglés mejor conocido como físico y matemático, nacido en el año 1643, en Woolsthorpe, Inglaterra, desarrolló las ideas de Galileo Galilei y sus estudios publicados en el libro Principios matemáticos de filosofía natural, en el que describía sus estudios y descubrimientos en la gravitación Universal y describió las tres leyes fundamentales del movimiento, llamado las leyes de Newton.

Las tres leyes son:
  • Principio de Inercia o Primera Ley de Newton;
  • Principio fundamental de la dinámica y la segunda ley de Newton;
  • Principio de Acción y Reacción o tercera ley de Newton.



LEYES DE NEWTON


  • Primera ley de Newton o ley de la Inercia:
La primera ley del movimiento rebate la idea aristotélica de que un cuerpo sólo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:
Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él





  • Segunda ley de Newton o ley del Movimiento:
La segunda ley del movimiento de Newton dice que
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.



  • Tercera ley de Newton o ley de acción y reaccion
Con toda acción ocurre siempre una reacción igual y contraria: o sea,
las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en
sentido opuesto




FUERZAS MECÁNICAS ESPECIALES


Las fuerzas mecánicas especiales, son fuerzas que por la forma en que actúan sobre otros cuerpos, presentan características diversas y se hace necesario diferenciarlas por su efecto, diagrama y sentido. Entre estas fuerzas encontramos las siguientes:


1
  • PESO DE UN CUERPO
El peso de un cuerpo es la fuerza que ejerce la tierra sobre los objetos, seres de la naturaleza que se encuentran en su superficie debido a la atracción gravitacional. 
El peso es la fuerza con que la Tierra nos atrae a su superficie. Esta se dirige hacia el centro de nuestro cuerpo celeste.
 matemáticamente se expresa como:

P⃗ =−G⋅M⋅mr2⋅u⃗ r
donde:
  • M es la masa del cuerpo, generalmente un cuerpo celeste como la Tierra, la Luna, el Sol, etc.,  que ejerce fuerza sobre otra masa m
  • r es la distancia que las separa.
  • u⃗ r es un vector unitario que expresa la dirección de actuación de la fuerza.
Tal y como vimos en el apartado de fuerza gravitatoria, la gravedad es la aceleración con que un cuerpo atrae a otro por la acción de la fuerza gravitatoria y su expresión es:
g⃗ =−G⋅MTrT2⋅u⃗ r
Sustituyendo el valor de la gravedad, en la expresión del peso obtenemos una expresión más simplificada y comunmente utilizada:

P⃗ =m⋅g⃗ 
donde:
  • m es la masa del cuerpo que sufre la fuerza gravitatoria.
  • g⃗  es la gravedad en el punto en el que se encuentra dicho cuerpo
En concreto su módulo es
P=m⋅g

Diferencias entre masa y peso

  • La unidad de medida en el S.I. de masa es el kilogramo (Kg), mientras que el peso se mide en Newtons (N).
  • El peso es una magnitud vectorial, mientras que la masa es una magnitud escalar.
  • Sólo podemos hablar de peso cuando el cuerpo se encuentra en un lugar donde hay gravedad. En la Tierra esta gravedad tiene un valor aproximado g = 9.8 m/s2 en los puntos próximos a la superficie terrestre. Cuanto más alejados del centro de la Tierra nos encontremos, menor será nuestro peso, ya que la gravedad disminuye a medida que nos alejamos de dicho centro.  
  • La masa de un cuerpo es inherente a él independientemente de si existe gravedad o no.
  • Si quieres conocer la masa puedes utilizar un instrumento de medida de masas como la balanzamientras que para conocer el peso se utilizan instrumentos de medidas de fuerzas, tales como eldinamómetro.

Ejemplo:
cual será el cuerpo de una persona de 70 kg en la superficie de la tierra y a 500 km de altura?.
masa de la tierra: 6·1024 kg. Radio de la Tierra: 6370 Km.




  • FUERZA  NORMAL
Es la fuerza ejercida por una superficie sobre los cuerpos que se encuentra apoyados en ella. Se representa con la letra griega (N).

Cómo calcular la fuerza normal?
La fuerza normal no tiene una expresión general a partir de la cual podemos calcular directamente su valor, sin embargo se puede deducir para cada caso de estudio haciendo uso del principio fundamental o segunda ley de Newton.
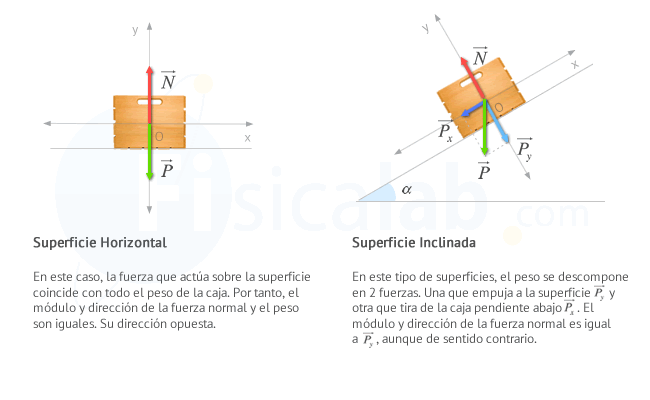
En este caso, la fuerza que actúa sobre la superficie coincide con todo el peso de la caja. Por tanto, el módulo y dirección de la fuerza normal y el peso son iguales. Su dirección opuesta.
Ejemplo:
Sabiendo que la fuerza normal de un cuerpo que se encuentra en un plano inclinado de 40º es de 150 N. ¿Cuál es su masa?

  • FUERZA DE TENSIÓNES
la fuerza que ejerce una cuerda, considerada de masa despreciable e inextensible, sobre un cuerpo que está ligado a ella. Se representa con la letra (T).
s. Cada tensión sigue la dirección del cable y el mismo sentido de la fuerza que lo tensa en el extremo contrario.
Por tanto, cada uno de los cuerpos que se encuentren unidos a los extremos de un cable tenso sufrirán la acción de una fuerza denominada tensión cuya dirección es idéntica a la del cable y su sentido equivalente al de la fuerza aplicada en el objeto del otro extremo y que provoca que el cable se tense. 
Por simplicidad, se suele suponer que las cuerdas tienen masa despreciable y son inextensibles (no se pueden deformar), esto implica que el valor de la tensión es idéntica en todos los puntos de la cuerda y por tanto, las tensiones que se ejercen sobre los cuerpos de ambos extremos de la cuerda son del mismo valor y dirección aunque de sentido contrario.
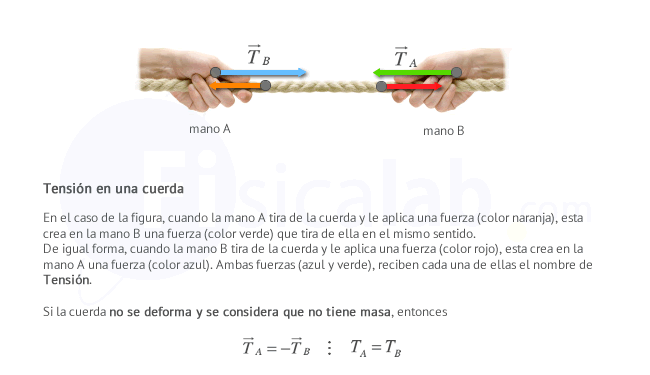
En el caso de la figura, cuando la mano A tira de la cuerda y le aplica una fuerza (color naranja), esta crea en la mano B una fuerza (color verde) que tira de ella en el mismo sentido. De igual forma, cuando la mano B tira de la cuerda y le aplica una fuerza (color rojo), esta crea en la mano A una fuerza (color azul). Ambas fuerzas (azul y verde), reciben cada una de ellas el nombre de Tensión. Si la cuerda no se deforma y se considera que no tiene masa, entonces ambas tensiones son iguales

¿Por qué las tensiones son iguales si la masa de la cuerda es despreciable?

Para contestar a esta pregunta, lo mejor es demostrarlo con un ejemplo. Cuando tiramos hacia arriba con suficiente fuerza del extremo de una cuerda o cable que tiene un cuerpo atado al otro extremo, y esta se tensa, conseguiremos mover el cuerpo. Veamos las fuerzas que intervienen en dicho movimiento.
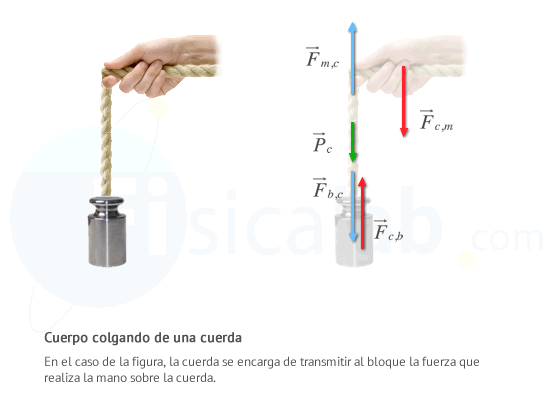
En el caso de la figura, la cuerda se encarga de transmitir al bloque la fuerza que realiza la mano sobre la cuerda.
Por un lado, la mano tira de la cuerda con una fuerza F⃗ m,c y según el principio de acción reacción, la cuerda ejercerá una fuerza sobre la mano F⃗ c,m en sentido contrario. Por otro lado, la cuerda tira del cuerpo con una fuerza F⃗ c,b y por reacción, el cuerpo ejerce una fuerza contraria sobre la cuerda F⃗ b,c. Adicionalmente, no debemos olvidar que sobre la cuerda actúa su peso P⃗ c.
Si consideramos que la masa de la cuerda es despreciable (mc = 0) y aplicamos la segunda ley de Newton a la cuerda, obtenemos que:
F⃗ m,c+F⃗ b,c+P⃗ c=mc⋅a⃗ c ⇒Fm,c−Fb,c+mc⋅g=mc⋅ac ⇒Fm,c = Fb,c

Si sabemos que la tensión (T) es la fuerza con que tira la cuerda a los objetos que se encuentran unidos a sus extremos, entonces:


Ejemplo:
Una bola metálica de 1 kg de masa se encuentra en reposo colgando del techo de una habitación por medio de una cuerda de 2 m de longitud. Si la masa de la cuerda es despreciable e inextensible. ¿Cuál es el valor de la tensión de la cuerda?
Encuentra a qui la solucion del ejercicio



  • FUERZA DE FRICCIÓN O ROZAMIENTO

Es la fuerza que ejerce la superficie de contacto, en sentido contrario al movimiento, sobre los cuerpos  que se muevan sobre ella. Se representa con la letra (fr). y se calcula con la expresión fr =μN, donde μ es el coeficiente de rozamiento y N la nomal. Este fenómeno se deba a que las superficies de contacto no son perfectamente lisas, sino que presentan rugosidades que encajan aleatoriamente entre sí, produciendo esta fuerza que se opone al movimiento.
Las leyes clásicas del rozamiento describen los factores de los que depende la fuerza de rozamiento. Fueron enunciadas por Guillaume Amontons (1663-1705) y Charles Augustin de Coulomb (1736-1806) y establecen que:
  • La fuerza de rozamiento entre dos cuerpos es proporcional a la fuerza normal que ejerce un cuerpo sobre el otro.
  • La fuerza de rozamiento no depende del área de contacto de ambos cuerpos, aunque sí de la naturaleza de sus materiales.
  • La fuerza de rozamiento no depende de la velocidad a la que se deslicen los cuerpos.
  • La fuerza de rozamiento tiene sentido opuesto al movimiento (a la velocidad).
Partiendo de estos factores, matemáticamente la fuerza de rozamiento se obtiene por medio de la siguiente expresión:

F⃗ r=−μ⋅N⋅u⃗ v
donde:
  • F⃗ r es la fuerza de rozamiento.
  • μ es el coeficiente de rozamiento. Se trata de un valor adimensional que depende de la naturaleza y del tratamiento de las sustancias que están en contacto.
  • N es el módulo de la fuerza normal.
  • u⃗ v es un vector unitario en la dirección y sentido del vector velocidad.
Observando la ecuación anterior, podemos concluir que su módulo es:

Fr=μ⋅N


Ejemplo:
Un caja de 60 kg de masa se encuentra en reposo sobre un suelo horizontal que posee un coeficiente estático de rozamiento de 0.6 y cinético de 0.25. Calcular:
a) La fuerza mínima necesaria para comenzar a mover la caja
b) La fuerza de rozamiento y la aceleración de la caja si se aplica una fuerza horizontal de 400 N

  • FUERZAS ELÁSTICAS RECUPERADORAS

Según el principio de acción reacción o tercera ley de Newton, en cada interacción existen dos fuerzas. Esto implica que si ejercemos una fuerza sobre un muelle, este último ejercerá también sobre nosotros otra fuerza de igual dirección y módulo aunque de sentido contrario. Dicha fuerza, recibe el nombre de fuerza elástica o restauradora.
La fuerza elástica es la fuerza que ejerce un muelle que no ha superado su límite de elasticidad y sufre una fuerza que lo deforma temporalmente.
F⃗ e=−k⋅x⃗ 
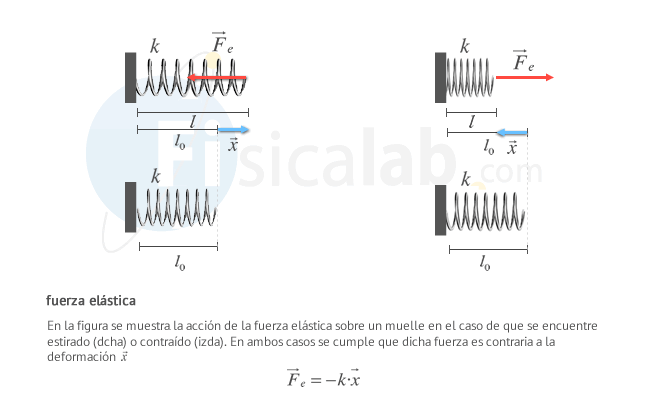
Fuerza elástica. En la figura se muestra la acción de la fuerza elástica sobre un muelle en el caso de que se encuentre estirado (dcha) o contraído (izda). En ambos casos se cumple que dicha fuerza es contraria a la deformación

Características de la fuerza elástica


  • Su dirección sigue el eje longitudinal del muelle.
  • Su sentido es contrario a la deformación que sufre el muelle.
  • Su módulo se puede obtener por medio de la siguiente expresión: Fe=k⋅x.
Ejemplo.
En un plano inclinado de 30º se encuentra un bloque de piedra de 100 Kg en reposo sujetado por un muelle cuya constante elástica es 2500 N/m. Suponiendo que no existe rozamiento determinar la elongación del muelle.
SOLUCION:      encuentra aqui la solucion del ejercicio
  • FUERZA CENTRÍPETA Y CENTRÍFUGA
Cuando una partícula describe un movimiento circular uniforme, posee una aceleración dirigida hacia el centro de la trayectoria de magnitud , esta  aceleración centrípeta está relacionada con el cambio de la dirección de la velocidad tangencial o lineal de la partícula. De acuerdo a la segunda ley de Newton ;  o .Por tanto la fuerza centrípeta es la  fuerza resultante que provoca la aceleración centrípeta y a la fuerza de reacción a ésta se le llama fuerza centrífuga.Resultado de imagen para imagenes de la fuerza centripeta y centrifuga
F⃗ n=m⋅a⃗ n=m⋅v2ρ⋅u⃗ n

Donde:
  • F⃗ n : Es la fuerza centrípeta. Se suele usar el subíndice n por que su dirección es normal a la trayectoria y de esta manera se la diferencia de la fuerza centrífuga. Su sentido, al igual que el de la aceleración centrípeta, apunta hacia el centro de curvatura. Su unidad de medida en el Sistema Internacional (S.I.) es el newton (N)
  • m: Masa del cuerpo. Su unidad de medida en el Sistema Internacional (S.I.) es el kilogramo (kg)
  • a⃗ n : Aceleración normal o centrípeta. Su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s2) y su valor viene dado por an=v2/ρ siendo v la velocidad del cuerpo en ese punto ρ y el radio de curvatura
Ejemplo:
La fuerza con que el Sol atrae a la Tierra. Esta fuerza es la fuerza centrípeta responsable del movimiento circular de la Tierra alrededor del Sol.
un ejemplo de fuerza centrifuga es a rotación elíptica de los planetas respecto a su estrella.
Característica de la Fuerza

  1. Magnitud: consiste en el mayor o menor grado de fuerza aplicada para producir un cambio de forma o movimiento. También es conocida como la intensidad que representa la cantidad de fuerza aplicada sobre el objeto.
  2. Dirección: establece la  o trayectoria en que se mueve el cuerpo por efecto o aplicación de la fuerza, según los  cardinales.
  3. Sentido: nos indica hacia donde se aplica la fuerza, para cada dirección hay siempre dos sentidos, de los cuales se toma como positivas las fuerzas que actúan en un sentido y negativas las que actúan en sentido opuesto al positivo.
  4. Punto de aplicación: es la zona, lugar, sitio donde se ejerce o aplica la fuerza al objeto.



Teorema del seno

Cada lado de un triángulo es directamente proporcional al seno del ángulo opuesto.
teorema de los senos
Teorema del coseno
En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.
del coseno



video desarrollando algunos Ejemplos de las leyes de Newton 



PREZI SOBRE TRABAJO, POTENCIA Y ENERGIA




CALCULO DE LA GRAVEDAD DE NEIVA 







BIBLIOGRAFIA


Referencias tomadas respetando el derecho del autor  con fines exclusivamente  educativos.





Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)